专题03四边形中常见的几种模型中点四边形模型1.(2021秋·河南郑州·九年级校考期中)如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( )A.一定不是平行四边形B.一定不是中心对称图形C.当AC=BD时,它是轴对称图形D.当AC=BD时,它是矩形【答案】C【分析】先连接AC,BD,根据EF=HG=AC,EH=FG=BD,可得四边形EFGH是平行四边形可判断A,根据平行四边形是中心对称图形,四边形EFGH是平行四边形是中心对称图形可判断B,当AC=BD时,EF=FG=GH=HE,此时四边形EFGH是菱形,据此可判断C,只有AD⊥BD时是矩形,当AC与BD不垂直时,不是矩形可判断D即可.【详解】解:连接AC,BD交于O,AC交GF于M,DB交EF于N,如图:∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,∴EF=HG=AC,EH=FG=BD,EF∥AC,GF∥DB,∴四边形EFGH是平行四边形,故选项A错误;∵平行四边形是中心对称图形,∴四边形EFGH是平行四边形,∴四边形EFGH是中心对称图形,故选项B错误;当AC=BD时,EF=FG=GH=HE,此时四边形EFGH是菱形,菱形是轴对称图形,∴菱形EFGH是轴对称图形,故选项C正确;只有AC⊥BD时∠MON=90°,∵GF∥DB,∴AC⊥GF,∴∠OMF=90°,∵EF∥AC,∴BD⊥EF,∴∠ONF=90°,∴∠NFM=360°-∠MON-∠OMF-∠ONF=90°,∴平行四边形GHEF是矩形,当AC与BD不垂直时,∵GF∥DB,EF∥AC,∴四边形ONFM为平行四边形,∠MFN=∠MON≠90°,即∠GFE≠90°,∴平行四边形GHEF不是矩形,故选项D错误.故选:C.【点睛】本题主要考查了中点四边形的运用,轴对称识别,中心对称识别,矩形判定,三角形中位线性质解题时注意:平行四边形是中心对称图形.解决问题的关键是掌握三角形中位线定理.2.(2022秋·广东佛山·九年级统考期中)若顺次连接四边形ABCD四边中点所得的四边形是正方形,则四边形ABCD一定满足( )A.是正方形 B.AB=CD且AB∥CD C.是矩形 D.AC=BD且AC⊥BD【答案】D【分析】首先根据题意画出图形,再由四边形EFGI是正方形,那么∠IGF=90°,IE=EF=FG=IG,而G、F是AD、CD中点,易知GF是△ACD的中位线,于是GFAC,GF=AC,同理可得IGBD,IG=BD,易求AC=BD,又由于GFAC,∠IGF=90°,利用平行线性质可得∠IHO=90°,而IGBD,易证∠BOC=90°,即AC⊥BD,从而可证四边形ABCD的对角线互相垂直且相等.【详解】解:如图所示,四边形ABCD的各边中点分别是I、E、F、G,且四边形EFGI是正方形,∵四边形EFGI是正方形,∴∠IGF=90°,IE=EF=FG=IG,又∵G、F是AD、CD中点,∴GF是△ACD的中位线,∴GFAC,GF=AC,同理有IGBD,IG=BD,∴AC=BD,即AC=BD,∵GFAC,∠IGF=90°,∴∠IHO=90°,又∵IGBD,∴∠BOC=90°,即AC⊥BD,故四边形ABCD的对角线互相垂直且相等,即:AC=BD且AC⊥BD.故选:D.【点睛】本题考查了中点四边形,正方形的性质、三角形中位线定理、平行线性质.解题的关键是连接AC、BD,构造平行线.3.(2018春·江苏无锡·九年级校考期中)如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于cm.【答案】8【分析】连接AC、BD,根据矩形的性质可得AC=BD,根据三角形中位线的性质可得HG=EFAC,EH=FGBD,根据四边形EFGH的周长为16cm列式求解即可.【详解】解:如图,连接AC、BD,∵四边形ABCD是矩形,∴AC=BD,∵E、F、G、H分别是AB、BC、CD、DA的中点,∴HG=EFAC,EH=FGBD,∴四边形EFGH的周长等于HG+EF+EH+FG=4AC=16,则AC=8cm.故答案为:8.【点睛】本题考查矩形的性质,三角形的中位线的应用,解题的关键是掌握三角形中位线定理.三角形的中位线平行于第三边,并且等于第三边的一半.4.(2022春·江苏扬州·八年级统考期中)阅读下面材料:在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?小敏在思考问题时,有如下思路:连接AC.结合小敏的思路作答:(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;(2)如图2,在(1)的条件下,若连接AC,BD.①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.【答案】(1)是平行四边形,理由见解析;(2)①AC=BD;证明见解析;②AC⊥BD.【分析】(1)如图2,连接AC,根据三角形中位线的性质及平行四边形判定定理即可得到结论;(2)①由(1)知,四边形EFGH是平行四边形,且FG=BD,HG=AC,于是得到当AC=BD时,FG=HG,即可得到结论;②若四边形EFGH是矩形,则∠HGF=90°,即GH⊥GF,又GH∥AC,GF∥BD,则AC⊥BD.【详解】解:(1)是平行四边形.理由如下:如图2,连接AC,∵E是AB的中点,F是BC的中点,∴EF∥AC,EF=AC,同理HG∥AC,HG=AC,∴EF∥HG,EF=HG,∴四边形EFGH是平行四边形;(2)①AC=BD.理由如下:由(1)知,四边形EFGH是平行四边形,且FG=BD,HG=AC,∴当AC=BD时,FG=HG,∴平行四边形EFGH是菱形;②当AC⊥BD时,四边形EFGH为矩形.理由如下:同(1)得:四边形EFGH是平行四边形,∵AC⊥BD,GH∥AC,∴GH⊥BD,∵GF∥BD,∴GH⊥GF,∴∠HGF=90°,∴四边形EFGH为矩形.【点睛】此题主要考查了中点四边形,熟练掌握三角形中位线定理及平行四边形、菱形及矩形的判定是解题的关键.“十字架”模型5.(2021春·安徽淮南·八年级校联考期中)数学活动:探究正方形中的十字架(1)猜想:如图1,在正方形ABCD中,点E、F分别在CD、AD边上,且BF⊥AE,猜想线段AE与BF之间的数量关系:.(2)探究:如图2,在正方形ABCD中,点E、F、G、H分别在AB,BC,CD,AD边上,且EG⊥HF,此时线段HF与EG相等吗?如果相等请给出证明,如果不相等请说明理由.(3)应用:如图3,将边长为4的正方形纸片ABCD折叠,使点A落在CD边的中点E处,点B落在点F处,折痕为MN,则线段MN的长为.【答案】(1)AE=BF;(2)HF=EG,证明见解析;(3)【分析】(1)利用AAS证明△ABF≌△DAE,即可得到结论;(2)过点E作EM⊥CD,垂足为M,过点H作HN⊥BC,垂足为N,利用ASA证明△HFN≌△EGM,即可得到结论;(3)连接NE,作NP⊥AD交AD于点P,根据折叠的性质,利用勾股定理就可以列出方程,从而解出DM的长,在Rt△EFN和Rt△NEC中,得到EF2+FN2=CE2+CN2,求出FN,再利用勾股定理即可求出MN.【详解】解:(1)AE=BF,∵四边形ABCD是正方形,∴AD=AB,∠BAF=∠ADE=90°,∴∠DAE+∠AED=90°,∵BF⊥AE,∴∠AFB+∠DAE=90°,∴∠AED=∠AFB,在△ABF和△DAE中,,∴△ABF≌△DAE(AAS),∴BF=AE;(2)EG=HF,理由是:如图,过点E作EM⊥CD,垂足为M,过点H作HN⊥BC,垂足为N,∵四边形ABCD是正方形,∴EM=HN,∵∠EPQ=90°,∴∠PEQ+∠PQE=90°,又EM∥BC,∴∠PQE=∠HFN,∴∠PEQ+∠HFN=90°,又∠HFN+∠FHN=90°,∴∠PEQ=∠FHN,在△HFN和△EGM中,,∴△HFN≌△EGM(ASA),∴HF=EG;(3)如图,连接NE,作NP⊥AD交AD于点P,由四边形ABCD是正方形及折叠知,FN=BN,EM=AM,EF=AB,∠EFN=∠B=90°,在Rt△DEM中,DM2+DE2=EM2,∵AB=BC=CD=DA=4,E为BC的中点,∴DE=2,∴DM2+22=(4-DM)2,解得DM=,在Rt△EFN中,EF2+FN2=EN2,在Rt△NEC中,CE2+CN2=EN2,∴EF2+FN2=CE2+CN2,∴42+FN2=22+(4-FN)2,解得,FN=,∴BN=AP=,∴MP=AD-DM-AP=4--=2,在Rt△MPN中,MN==.【点睛】本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,翻折变换的问题,找到相应的直角三角形利用勾股定理求解是解决本题的关键.6.(2022秋·甘肃兰州·九年级校考期中)如图,在矩形的边上取一点,连接,使得,在边上取一点,使得,连接.过点作于.(1)求证:四边形是菱形;(2)若,,求的长.【答案】(1)见解析(2)的长为【分析】(1)根据矩形的性质判定四边形是平行四边形,再根据,即可得到结论;(2)根据矩形和菱形的性质证明,对应边成比例即可求出的长.【详解】(1)证明:四边形是矩形,,,,即,四边形是平行四边形,,四边形是菱形;(2)解:四边形是矩形,,在Rt中,,,根据勾股定理得,,四边形是菱形,,,,,,,,,即,.【点睛】本题考查了矩形的性质,菱形的判定与性质,勾股定理,相似三角形判定与性质,解决本题的关键是综合运用以上知识.对角互补模型7.(2022秋·山东枣庄·九年级统考期中)定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.根据以上定义,解决下列问题:(1)如图1,正方形中是上的点,将绕点旋转,使与重合,此时点的对应点在的延长线上,则四边形______(填“是”或“不是”)“直等补”四边形;(2)如图2,已知四边形是“直等补”四边形,,,过点作于点.①试探究与的数量关系,并说明理由;②若,,求的长.【答案】(1)是;(2)①BE=DE,理由见解析;②14【分析】(1)由旋转的性质可得∠ABF=∠CBE,BF=BE,根据正方形的性质得∠ABC=∠D=90°,可得出∠EBF=∠D=90°,即可得出答案;(2)①过点C作CF⊥BE,首先证明四边形CDEF是矩形,则DE=CF,EF=CD=2,再证△ABE≌△BCF,根据全等三角形的判定和性质可得BE=CF,AE=BF,等量代换即可得BE=DE;②设BE=x,根据勾股定理求出x的值即可,即可求解.【详解】(1)∵将△BCE绕B点旋转,BC与BA重合,点E的对应点F在DA的延长线上,∴∠ABF=∠CBE,BF=BE,∵四边形ABCD是正方形,∴∠ABC=∠D=90°,∴∠ABE+∠CBE=90°,∴∠ABE+∠ABF=90°,即∠EBF=∠D=90°,∴∠EBF+∠D=180°,∵∠EBF=90°,BF=BE,∴四边形BEDF是“直等补”四边形.故答案为:是;(2)①BE=DE,理由如下:如图3,过点C作CF⊥BE,垂足为点F, 图3∵四边形ABCD是“直等补”四边形,AB=BC,AD>AB,∴∠ABC=90°,∠ABC+∠D=180°,∴∠D=90°,∵BE⊥AD,CF⊥BE,∴∠DEF=90°,∠CFE=90°,∴四边形CDEF是矩形,∴DE=CF,EF=CD,∵∠ABE+∠A=90°,∠ABE+∠CBE=90°,∴∠A=∠CBF,∵∠AEB=∠BFC=90°,AB=BC,∴△ABE≌△BCF(AAS),∴BE=CF,AE=BF,∵DE=CF,∴BE=DE;②如图3,∵四边形
2023年数学九年级上册北师大版专题03 四边形中常见的几种模型(解析版)
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
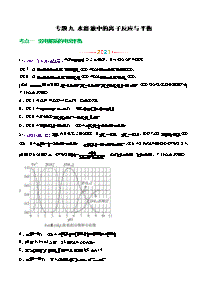
2023年数学九年级上册北师大版专题13 反比例函数的应用(解析版)
2023-11-10 21:43
 35页
35页 -
2023年数学九年级上册人教版专题01 一元二次方程及其解法(原卷版)(人教版)
2023-11-10 21:45
 3页
3页 -
2023年数学九年级上册人教版专题02 一元二次方程的应用(原卷版)(人教版)
2023-11-10 21:45
 6页
6页 -
2023年数学九年级上册人教版专题01 一元二次方程及其解法(解析版)(人教版)
2023-11-10 21:45
 11页
11页 -
2023年数学九年级上册苏科版专题01 一元二次方程(经典基础题7种题型+优选提升题)(原卷版)
2023-11-10 21:45
 14页
14页 -
2023年数学九年级上册苏科版专题01 一元二次方程(经典基础题7种题型+优选提升题)(解析版)
2023-11-10 21:45
 27页
27页 -
2023年数学九年级上册人教版专题02 一元二次方程的应用(解析版)(人教版)
2023-11-10 21:45
 15页
15页 -
2023年数学九年级上册人教版专题03 二次函数的图像与性质(原卷版)(人教版)
2023-11-10 21:45
 5页
5页


 U1
U1